Newみんなの算数講座60 美しき平行四辺形のグラフ

こんにちは。ニューみんなの算数講座は今回がキリよく60講座目です。記念回というほどでもないですが、速さのジャンルからみなさんの印象に残りそうな問題を用意しました。わりと手ごわい問題で、初めて解いて正解するのはけっこう大変だと思います。僕も若い時分、初見のときには解けなかったです。ぜひ一度経験しておいてほしいと思います。

ではその問題を出しますよ？

問題文長いですよね。読むだけで疲れちゃいました？(笑) がんばってもう一度問題の意味を確認しましょうか。
全員が車に乗れないから、Ａ地点出発と同時にグループはふたてに分かれ、片方のグループは車で、もう片方のグループは徒歩でＢ地点に向かいます。当然車の方が速いから、おじさんは途中で３人を下ろして徒歩組を迎えにいきます。そして徒歩組を見つけて車に乗せると再度Ｂ地点に向かった。その結果２つのグループが同時にＢ地点に着いたということです。設定が非現実的すぎるって？ ははは。そうですね。まあそこは算数の問題ですから(^^)/

状況を図示する直線図を作ってみました。実線が車で点線が徒歩です。色分けは同じ色のところが同じ時間を示しています。しかしこの問題はこうした直線図だけでは手がかりがつかみにくいのです。せっかく作りましたけど、この図を使うのはやめましょう。

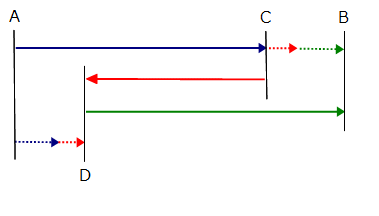
では正しい図の書き方をお伝えしますね。じつはこの問題、横軸を時間、タテ軸を距離にしたグラフを書くと、その状況がとても美しい平行四辺形のグラフになります。改めて作り直しました。下のようなグラフです。

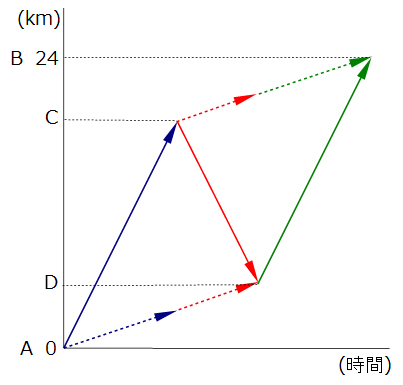
ボツにした最初の図と同じように、車の進行を実線、歩く子供を点線にしました。時間の流れを色で区別しています。
青　車がＣ地点で子供を降ろすまで
赤　引き返した車がＤ地点で子供を拾うまで
緑　Ｂ地点に到着するまで
です。

なぜこのような平行四辺形のグラフになるかといえば、全員が同時にＢ地点に着いたということは「２つの子供たちのグループが車に乗っていた時間と歩いていた時間が同じだから」です。
もし車に乗っていた時間と歩いた時間が違えば、２つのグループが同時にＢ地点に着くことはありません。車に乗っていた時間が長いグループが先にＢ地点に着くはずですね。２つのグループが同じ時間だけ車に乗って、同じ時間だけ歩いたから上のような美しい平行四辺形のグラフになるわけです。

ではいよいよ解答を求めましょう。
徒歩の速さ：車の速さ＝４km/時：36km/時＝１：９です。
進むのに経過した時間が等しいとき、進んだ距離は速さの比が示すから、
徒歩組がＡＤを歩いた距離を１とすると、
車がＡＣを進んだ距離とＣＤを戻った距離の和が９になります。

くわしく　徒歩組がＡからＤまで歩いたのと同じ時間で、車はＡからＣまで行き、さらにＣからＤへ戻っています。

この１と９を使って、解答に必要ないくつかの距離を表現します。
ＣＤ間の距離は(９－１)÷２＝４
ＡＢ間の距離は１＋４＋１＝６
クルマが走った距離の合計は９＋４＋１＝14です。
＊平行四辺形グラフの形状から、ＢＣ間の距離とＡＤ間の距離は同じです。

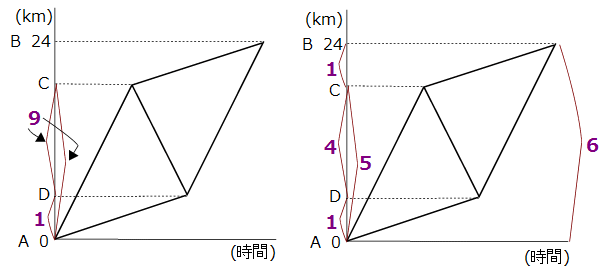
では解答へ最終着陸。

(1)
ＣＤ間の距離は、ＡＢ間の距離の4/6、約分して2/3です。
ＡＢ間の距離は24kmだからＣＤ間の距離は 24×2/3＝16kmです。

(2)
Ａ地点を出発してからＢ地点に着くまでにかかる時間は、車が走った距離の合計を車の速さで割れば求めることができます。
車が走った距離の合計はＡＢ間の距離の14/6倍、約分して7/3倍だから24×7/3＝56kmです。車の速さは時速36kmだから、56kmを走るのにかかる時間は56÷36＝56/36(時間)＝14/9(時間)＝１と5/9(時間)です。

美しき平行四辺形グラフの問題いかがでしたか？ 60講座の節目にこの問題を解説しようと決めて張り切ってグラフも作ってみましたが、一度読んだだけではちょっと…という方が多いかもしれません。正直簡単ではないと思います。まだ理解が不安な方は、このページを印刷して何度か落ちついて読んでみてくださいね。ストンと頭に落ちたときの爽快感は格別だと思いますよ。え？ 一回で理解できたって？ それはすごいなあ。算数のセンスがとても豊かな人だと思います(*^^)

では今回の講座はここまでにしますね。次回の講座は、元祖を修理して残すか新作に差し替えるか思案橋中です。早めに発表しますからね。乞うご期待です！