Newみんなの算数講座49 エラトステネスのふるい

こんにちは～。ニューみん算講座49の時間です。

今回は問題の解き方の解説ではなく、算数を勉強していく上で知っておくといいかな？というお話をしようと思います。自然数を２つのチームに分類するお話ですね。片方が素数チーム、もう片方が合成数チームです。

素数は講座１、２、38などで活躍しましたね。素数は１とその数自身以外に約数を持たない自然数です。逆に素数ではない自然数のことを合成数といいます。つまり素数と合成数は対義語ですね。なお、１は素数でも合成数でもない中立の数です。だから正確に言えば、自然数は１か素数か合成数ということになりますね。え？ ０ですか？ ０は整数には入るけど自然数には入らないのです。今回の話は自然数の範囲で考えるから０のことは気にしないで大丈夫です。０より小さいマイナスの整数も算数では想定しないことになってます。

〈整数と自然数の違い〉
整数　０と、０に１ずつたしていくことで作れる数です。算数では想定しませんが、数学では０から１ずつ引いていくマイナスの整数も出てきます。
自然数　整数のうち、０とマイナスの整数を除いた数です。１以上の整数ですね。ものを数えるときに使う数という説明もあります。
算数では０を含めると整数、含めないと自然数ということですね。

さて今回のタイトルはエラトステネスのふるいです。エラトステネスは紀元前の学者で、地球の大きさを測定するなど、第二のプラトンと呼ばれるぐらい優秀だった人ですが、エラトステネスのふるいは彼が自然数を素数と合成数に分けるために考えた方法です。ふるいというのは右の写真のような道具のことで、穴より小さな物質を落とし、穴より大きい物質を残すためのものです。なぜふるいの名まえがついているか、説明を読むうちにわかると思います。

それではエラトステネスのふるいを開始します。範囲にきまりはないですが、ここでは100までの自然数を範囲にしました。

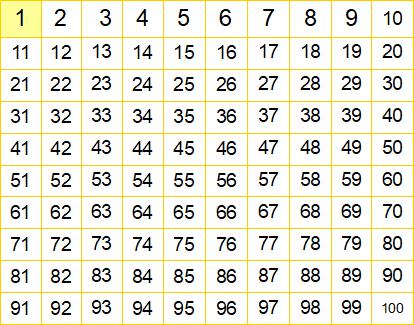
まず中立の１を除外しました。黄色い枠です。99個の自然数が残ってますね？ ここから合成数をふるい落としていきます。素数の２を残し、２の倍数は素数ではないからすべて消します。

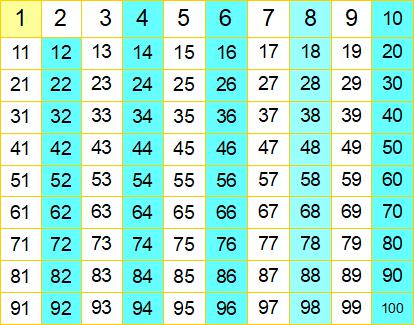
素数の２を除いた２の倍数49個を消しました。水色の枠です。ここでは色をつけたことを消したことだと考えてください。次に素数の３を残し、３の倍数は素数ではないからすべて消します。

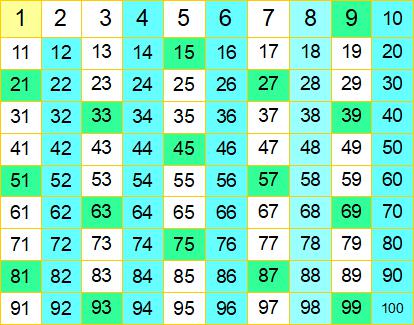
素数の３を除いた３の倍数を消しました。２の倍数のときに消えていた数もあり、いま消したのは緑色の枠の16個です。次は素数の５を残し、５の倍数は素数ではないから消します。

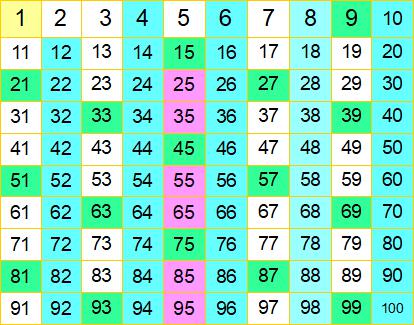
素数の５を除いた５の倍数を消しました。２の倍数や３の倍数のときに消えていた数もあり、新たに消したのは紫色の枠の６個です。次が最終段階になります。素数の７を残し、７の倍数は素数ではないから消します。

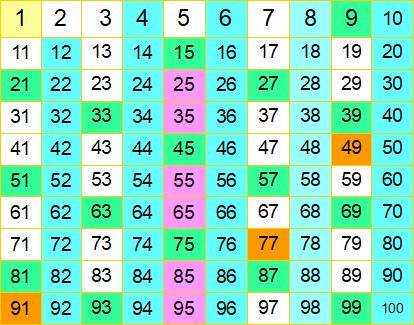
素数の７を除いた７の倍数を消しました。前段階で消えている７の倍数もあり、いま消したのは49、77、91の三つだけです。オレンジ枠です。49と91はウッカリ忘れやすい７の倍数なので記憶に留めておいてください。

100までの自然数を範囲にした場合、この時点で作業は終了となります。消えた数(色をつけた数)が合成数、白い枠のまま残っている数が素数です。100までの素数が25個というのは覚えておいてもよいでしょう。
ここで作業が終了する理由はわかりますか？ ７の次に小さい素数は11です。 11は素数として残っていますが、それ以外の11の倍数は、２の倍数のときに22が消え、３の倍数のときに33が消え、…というようにすでに全部消えてます。残っている11の倍数がないから消しようがないわけです。だから７の倍数を消した時点で操作は終了です。(消えているのは11に11より小さい素数をかけた11の倍数です。11×11、11×13などは残ってますが100までの範囲を超えてます)

ではエラトステネスのふるいについてまとめておきますね。

エラトステネスのふるい、なかなか面白いでしょう？ パネルクイズアタック25みたい？ 雰囲気ありますね(笑) じつは素数の世界にはいまだに未解決の謎もありましてね。たとえば 573491273 のような大きな数が素数かどうかを簡単に判定する方法は発見されていません。もしみなさんが発見したらフィールズ賞(数学のノーベル賞)は間違いないです(*^^)
算数ではそれほど大きな数の素数判定は必要ないと思いますが、100まで(できれば200まで)の自然数が素数かどうかは時間をかけずに判断できると便利ですね。100までなら今回の講座で素数かどうかを覚えられると思います。さらに範囲を広げた200までのふるい、ぜひみなさんがやってみてください。

それでは今回のお話はこれでおしまいです。次の講座から２回連続でＮ進法を予定しています。楽しみにしていてくださいね！