Newみんなの算数講座72 円すいマニュアル

みなさんこんにちは。ニューみん算講座72です。
元祖講座の72番は改訂して残すほどの内容ではなかったので、ここもまた新しい講座を書くことにしました。3回連続11本目の新作です。ニューみん算講座の新作率11÷72=0.152777… =約15%です。もともと元祖講座の二割ぐらいはボツにして書き直すつもりだったので、まだ少し足りてないけどだいたい予定通りです。しかし11÷72って0.152以下7の無限ループなんですね。この割り算をしたのは生まれて初めてだったかも~。何十年付き合っていても数には新しい発見があるな~と思いました(^^)/
さて今回の講座では立体図形の円すいを取り上げることにします。円すいの問題は算数のテストにかなりよく出てきますから、今回紹介するいくつかの計算方法は知らないとヤバい!というものばかりだと思います。算数の常識として頭に入れておいてくださいね。では問題を出しますよ。
下の図のように、底面の円の半径9cm、高さ12cm、母線の長さ15cmの円すいについて次のものを求めてください。円周率は3.14とします。
(1)体積
(2)展開図を書いたときの側面の中心角
(3)側面積
(4)表面積
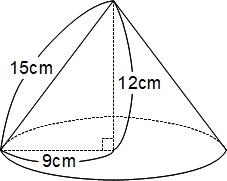
(1)
すいの体積は底面積×高さ×1/3です。
9×9×3.14×12×1/3=324×3.14=1017.36cm³
メモ すいの体積の1/3の理由を算数で一般的に説明するのは大変です。シンプルな形に限っては算数テクニック公式集で説明しています。算数ではそこからの類推で納得しておいてください。厳密な証明は高校数学の積分の領域です。
(2)
円すいの展開図は、下の図のように側面がおうぎ形、底面が円になります。
半径15cmのおうぎ形の弧の長さが半径9cmの底面の円の円周と等しくなるためには、側面のおうぎ形は全円に対して9/15倍の大きさでなくてはなりません。
展開図の中心角=360°×(底面の半径/母線の長さ) を覚えてください。
この場合、オレンジ色で示した側面の中心角は360°×9/15=360°×3/5=216°です。
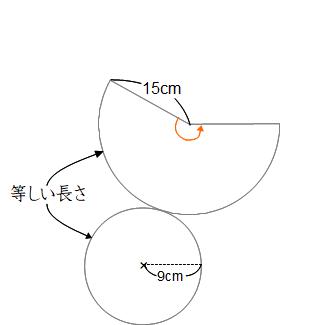
メモ 心配な人は、おうぎ形の弧の長さと円の円周が一致することを確認してみてください。
おうぎ形の弧の長さ=15×2×3.14×216/360=15×2×3.14×3/5=18×3.14
円の円周=9×2×3.14=18×3.14
ちゃんと等しくなりますね。
(3)
15×15×3.14×216/360を普通に計算してもかまいませんが、216/360という割合は (底面の半径/母線の長さ) すなわち9/15と一致しています。
つまり15×15×3.14×216/360という式は15×15×3.14×9/15と書くことができて、このように書くと15×15の片方が分母の15と約分できて消えるから、15×9×3.14という計算だけで済むことがわかります。
円すいの側面積=母線の長さ×底面の半径×3.14 を覚えておくと便利です。
この場合の側面積は 15×9×3.14=423.9cm²です。
(4)
円すいの表面積は側面積+底面積です。
側面積は 15×9×3.14=135×3.14
底面積は 9×9×3.14=81×3.14 です。
これらを分配法則(後記)でまとめて、
表面積は 135×3.14+81×3.14=(135+81)×3.14=216×3.14=678.24cm² です。
以上で問題は片づきましたが、算数で円が絡む問題に頻出する「3.14をかける計算」についてアドバイスしておきますね。
3.14テクその1 よく出てくる計算結果は暗記しよう!(特に受験生)
同じ式を出てくるたびに何度も計算するのはあまり要領がよくないです。だって毎度毎度同じ答えになるわけでしょう? よく出てくる式の計算結果は覚えてしまうとよいです。一番下に暗記をお勧めする計算結果を表にしました。
3.14テクその2 分配法則を使って「×3.14」の計算はなるべくまとめよう!
表面積や体積の問題で、求めるものが□×3.14と〇×3.14のように3.14をかけた数の合計のとき、両方のかけ算を別々に計算してたすのは得策ではないことが多いです。(それぞれの計算が簡単な場合はそれでもかまいませんが)
分配法則とは □×3.14+〇×3.14=(□+〇)×3.14 です。
項はいくつつながっていても同じです。項が3つなら
□×3.14+〇×3.14+△×3.14=(□+〇+△)×3.14 です。たし算のところは引き算でも大丈夫です。
□×3.14-〇×3.14=(□-〇)×3.14 ですね。
分配法則の計算例
3×3×3.14+4×4×3.14=9×3.14+16×3.14=(9+16)×3.14=25×3.14=78.5
*もし25×3.14の答えを覚えていれば筆算する必要は一切ないです。
3.14テクその3 分配法則の逆用も考えよう!
何かに3.14をかける計算で、分配法則の逆用が効率的なことはとても多いです。
分配法則の逆用とは (□+〇)×3.14=□×3.14+〇×3.14 です。
分配法則逆用の計算例
56×3.14=50×3.14+6×3.14=157+18.84=175.84
86×3.14=90×3.14-4×3.14=282.6-12.56=270.04 など
*水色の式は計算結果(下表)の暗記を推奨しています。たし算や引き算は暗算できるなら暗算、不安なら筆算してください。このような工夫で、計算間違いしやすいケタ数の多いかけ算をなるべく避けることが大事です。
では最後に僕が暗記をお勧めする「☆×3.14」の計算結果を書いておきますね。多いな~と感じたら〇をつけたものを優先して覚えましょう。表にないものは筆算でしょうけど、表になくても□倍や組み合わせがきくものもありますからね。□倍も組み合わせ方もさまざまな手がありますので、下の表を最低限の知識として覚えた上で、そのあとはみなさんがいろいろとアレンジしてください。
□倍の例
144×3.14は72×3.14の2倍です。
144×3.14=(72×3.14)×2=226.08×2=452.16
組み合わせの例
56×3.14は24×3.14と32×3.14の合計です。覚えている二つの結果を合計すれば未知のかけ算をする必要がなくなります。
56×3.14=24×3.14+32×3.14=75.36+100.48=175.84
| 〇2×3.14=6.28 | 〇24×3.14=75.36 |
| 〇3×3.14=9.42 | 〇25×3.14=78.5 |
| 〇4×3.14=12.56 | 27×3.14=84.78 |
| 〇5×3.14=15.7 | 〇32×3.14=100.48 |
| 〇6×3.14=18.84 | 〇36×3.14=113.04 |
| 〇8×3.14=25.12 | 〇48×3.14=150.72 |
| 〇9×3.14=28.26 | 54×3.14=169.56 |
| 〇12×3.14=37.68 | 64×3.14=200.96 |
| 〇15×3.14=47.1 | 72×3.14=226.08 |
| 〇16×3.14=50.24 | 75×3.14=235.5 |
| 〇18×3.14=56.52 | 96×3.14=301.44 |
今回の講座は易しかったと思いますがとても大事な内容です。円すいの〈体積の公式〉〈展開図の中心角の公式〉〈側面積の公式〉どれも忘れないでくださいね。表面積にはふつう公式は用意しないから、底面積と側面積を求めて合計してください。3.14のかけ算も算数ではたくさん覚えている人の方が得をしますね。時間を短縮できる上に、計算を間違えることも少なくなりますので(*^^)
では今回の講座72はここまでにします。次回もどうやら新作になりそうです。元祖の70番台の講座は冴えないのが多かったな~。講座の倦怠期だったのかな~?(汗) 内容はまだ未定なので発表を楽しみに待っていてくださいね。じゃあそのときにまた算数をご一緒しましょう。またね~!













