Newみんなの算数講座61 2点が動いて面積が変化して

みなさんこんにちは。お元気でお過ごしでしょうか。
前回方針を思案中と言っていた今回の講座61ですが、むかし書いた点の移動の講座を修理して残すことにしました。内容的にはテストによく出そうな良問ですよ。それにしてもむかし書いた講座は算数に関係ないおしゃべりが多くて修理に手間取りました。好きな番組の主題歌をyoutubeで貼っていたのは自分で読み返しておかしくなってしまいました。こちらの改訂ニュー講座は純粋に算数メインで書いていきたいから、おしゃべりはなるべく減らそうと思ってるんです。全然ないと冷たい感じになってしまうからたまには脱線させますけどね(*^^)
…というわけで、新作を書く倍ぐらい修理に時間がかかった講座61です。いつものように問題を出して始めることにしますね。いろいろ話がしたくて設問を作ってたら(5)までになってしまいました。大変かもしれませんが最後までがんばって読んで理解してくださいね。
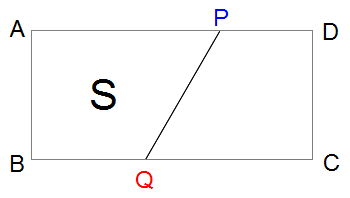
上の図のような長方形があり、点Pは頂点Aを出発して辺AD上を、点Qは頂点Bを出発して辺BC上をそれぞれ一定の速さで何度も往復します。2点P、Qを結ぶ直線の左側の図形をSとします。このとき、点Qが一往復を終えるまでの図形Sの面積は下のグラフのようになりました。
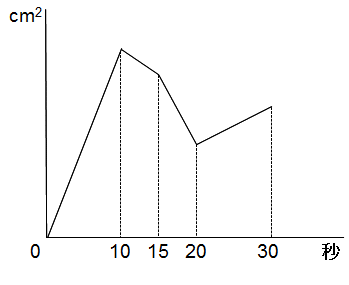
(1)点Pと点Qはどちらが速いですか?理由も答えてください。
(2)点Pと点Qの速さの比を求めてください。
(3)点P、Qが出発してから15秒後の図形Sの面積は36cm²でした。長方形ABCDの面積を求めてください。
(4)点Qが一往復するまでに、図形Sが長方形になることが2回あります。それは点P、Qが出発してから何秒後と何秒後ですか?
(5)点Pが一往復するまでに、図形Sの面積が長方形ABCDの半分になるときが2回あります。それは点P、Qが出発してから何秒後と何秒後ですか?
(1)
速いのは点Pです。おそらく正解率100%? しかし理由は問題図で点Pが点Qより右に書いてあるからではないですよ? 点Qは頂点Cに着くと折り返しますから、図の状況は先に頂点Cに着いた点Qが折り返したあとかもしれません。では点Pの方が速い正しい理由は?
問題文に「グラフは点Qが一往復を終えるまで」と書いてあります。点Qは往復に30秒かかっているから片道15秒です。ではその前の10秒のときになぜグラフが変化するのでしょうか? そうそう、10秒のときに点Pが頂点Dに着いたからですね。片道10秒の点Pと片道15秒の点Q。速いのは当然点Pです。
(2)
片道を点Pは10秒、点Qは15秒かかります。距離が等しいとき、速さの比と時間の比は逆比になるから、点Pと点Qの速さの比は時間の比(10:15=2:3)を逆にして3:2が正解です。
続く設問を処理するために、グラフが変化するところにア~エの記号をつけてみました。それぞれのところで何が起きたかを考えてみます。
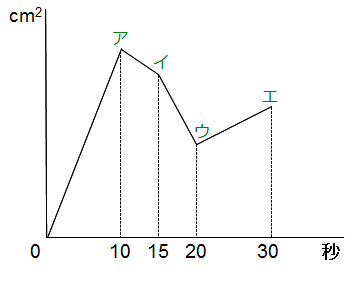
★グラフのアで起きたこと(10秒後)
点Pが頂点Dに到着しました。そのとき点QはBC上のBから2/3の地点でCに向かっています。(点Pと点Qの速さの比は3:2)
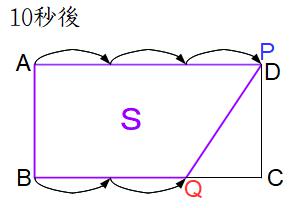
★グラフのイで起きたこと(15秒後)
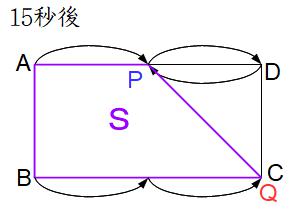
点Qが頂点Cに到着しました。点Pはすでに片道を終えて折り返し、DA上の中間点でAに向かっています。
〈中間点の理由〉点Pの速さは点Qの速さの1.5倍(3÷2=1.5)だから、点Qが片道を進めば点Pは片道の1.5倍を進みます。つまり点Pは片道を終えたあと、帰り道を半分進んでいます。
(3)
15秒後の図形Sの面積は長方形ABCDの面積の3/4です。このときの図形Sの面積が36cm²だから、逆算して長方形ABCDの面積は36÷3/4=48cm²です。
(4-1回目)
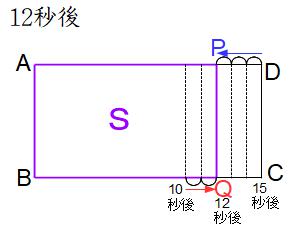
図形Sが長方形になるのは点Pの真下に点Qがくるときです。その1回目が10秒後と15秒後の間にあります。10秒後に点Pが頂点Dを折り返すと、点Pと点Qは向き合って進むことになり、両者の速さの比は3:2だから、下の図のように点Pが3マス、点Qが2マス進んで点Pの真下に点Qがきます。
点Qは5マス進むのに5秒(10秒後から15秒後まで)かかるから、2マス進むのには2秒かかり、点Pの真下に点Qがくるのは10+2=12(秒後)とわかります。
続いてグラフのウで起きたことを考えます。
★グラフのウで起きたこと(20秒後)
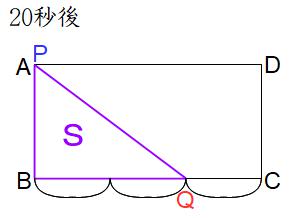
点Pが一往復を終えて点Aに戻りました。点Qはすでに折り返しを終え、Cから1/3の地点でBに向かっています。
〈点Qの位置〉点Qの速さは点Pの速さの2/3倍だから、点Pが片道を2回(往復)ぶん進むと、点Qは片道の2回×2/3=4/3回=1と1/3回ぶん進みます。つまり点Qは片道を終えたあと、帰り道を1/3だけ進んでいます。
(4-2回目)
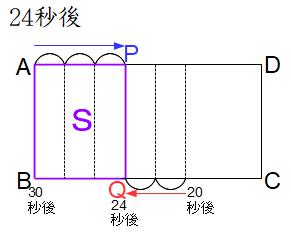
このあとに点Pの真下に点Qがきて、図形Sが長方形になる2回目があります。20秒後に点Pが頂点Aを折り返すと、点Pと点Qは向き合って進むことになり、さきほどと同様に点Pが3マス、点Qが2マス進んで点Pの真下に点Qがきます。点Qは5マス進むのに10秒かかるから、2マス進むのには10×2/5=4秒かかり、点Pの真下に点Qがくる2回目は20+4=24(秒後)とわかります。
(5-1回目)
PQが長方形ABCDの面積を二等分するのは、下の図のようにPQが長方形の対角線の交点を通るときです。この性質は長方形や平行四辺形の二等分でよく使うので覚えておいてください。点Pが進んだ距離と点Qが進んだ距離は3:2で、点Pは5進むのに10秒かかるから、3進むのには10×3/5=6秒かかります。1回目の解答は6秒後です。
*PQが長方形ABCDの対角線の交点を通ると、図形S(台形ABQP)と台形PQCDが上下を逆にした合同な図形になります。
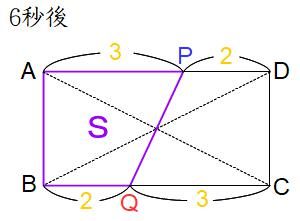
(5-2回目)
PQが長方形ABCDの面積を2回目に二等分するのは、15秒後に点Qが頂点Cを折り返した少しあと、点Pが一往復を終える少し前です。点Pが進んだ距離と点Qが進んだ距離は3:2です。これらを合計した5の距離はちょうど片道の3回ぶんです。もし点Pが5の距離を進むと30秒かかります(理由/点Pは片道を進むのに10秒。片道3回ぶんなら30秒)。実際に点Pが進んだ距離はその3/5倍だから、30秒×3/5=18秒より2回目の解答は18秒後です。
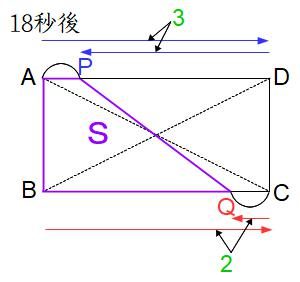
メモ 30秒後に点Qが一往復を終えたとき、点Pは一往復と片道を進んでいて、じつはこのときにもPQが長方形ABCDの面積を二等分します。これを除外するために(5)の条件を点Qが一往復を終えるまで(20秒後まで)としました。
ふ~ぅ。解説は以上です。書いていてくたびれました。みなさんも読んでいてくたびれたのではないでしょうか(*´з`) おそらくこうした問題はパソコンやモバイルでながめているだけですべて理解するのは厳しいでしょうから、ぜひカラー印刷が可能な環境で印刷し、ノートや白い紙に自分でも鉛筆を動かしながらじっくり読み直してもらえると理解がはかどると思います。それはこの講座に限らず、すべての講座にあてはまることかもしれませんね。お部屋でカラー印刷ができない場合は、会社ですとか、今はコンビニなどでもネットプリントといったサービスがありますから調べて使ってみるとよいと思います。
セブンイレブンのネットプリント
また、これは宣伝ですが一枚一枚カラー印刷してると手間がかかりますからね。僕の事務所で全講座をカラー印刷したものを販売してますから、もしよかったらこちらもご検討くださいね。102講座ぶんドカッと届けますよ(^^♪
Newみんなの算数講座カラー印刷ファイル購入
では講座61はこれで終わりにします。今回は宿題ありません。次回の講座は水ではなくて空気を見ようという体積の話ですね。楽しみに待っていてください。それじゃあまた~!
カーテンコール
最後に脱線。むかし書いた元祖講座61に貼っていた北の国からの主題歌です。この新サイトになってまだ一度もyoutubeを貼ってないから練習です。いや本当は懐かしくて残しておきたくなりました。youtubeだいぶ大きく出るんだなあ。サイズ変えても小さくなりません。勉強しますね。しかしいつ聴いてもいやされますね~(*^^*)













