Newみんなの算数講座27 食塩水と水の同量交換

今回は講座３のてんびん以来、二度目となる食塩水の問題です。正面からまともにぶつかる正攻法より時間をかなり短縮できるワザがあります。さてさてどういうことなのでしょう？

久々の食塩水はこんな問題です。

ワザの話はあと回しにして、まずはまともにぶつかってみましょう。

(1)
この表は生徒たちに好評です。ビーカーの図を書くより楽みたいですね。上の段から順に濃さ(%)、食塩水(g)、食塩(g)です。

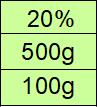
ではこの表を変化させていきますね。まず100gの食塩水を捨てます。濃さはそのままで食塩水が400ｇに減り、食塩も減りますね。

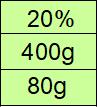
ここに水を100g加えると、食塩水は500gに戻りますが食塩はそのままです。

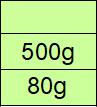
濃さ＝食塩÷食塩水 ですね。80÷500＝0.16 これを％に直して16％が正解です。

(2)
いまと同じことをあと２回繰り返せばいいですね。表を並べてみますから確認してください。

〈操作２回目〉

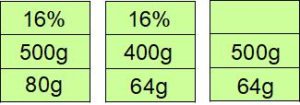
操作が２回終わったときの濃さは64÷500＝0.128＝12.8％です。

〈操作３回目〉

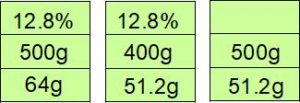
操作が３回終わると、食塩水の濃さは51.2÷500＝0.1024＝10.24％になります。これが正解です。

以上、ごく普通にぶつかる方法の解説でした。難しくないですよね。数字を間違えないようにていねいに計算すれば問題ないでしょう。表の書き方、よかったらマネしてくださいね。

でもかけ算やわり算の繰り返しが面倒だと感じた人もいると思います。なんかもっと簡単な方法がありそうですよね？
ちゃんとあるんです。せっかく僕の算数講座を読んでもらってますからね。みなさんにとって新しい知識になったらうれしいです。じゃあ近道を発表しますね。

さっそくこのワザを使ってみましょう。
上の問題では500gのうち100gを水と交換しました。もとの食塩水500gに対して残した食塩水は400gですね。この割合を最初の食塩水の濃さにかければ操作後の食塩水の濃さがわかります。

20(%)×400/500＝20×4/5＝16(%) →１回の操作後の濃さ

以下、何度繰り返しても同じ計算で大丈夫です。
16(%)×4/5＝16÷５×４＝3.2×４＝12.8(%) →操作２回後の濃さ

12.8(%)×4/5＝12.8÷５×４＝2.56×４＝10.24(%) →操作３回後の濃さ

ようは食塩水を400gから500gに増やしたとき、食塩水は4分の5倍になりますが、食塩の重さはそのままだから、濃さは逆の倍率の5分の4倍になるということなのです。複雑な理屈ではないですが、こうしたことを自分で気づいて使うのは大変ですね。ぜひ頭の片隅に残しておいてください。

食塩水と水の同量交換。理解していただけたでしょうか。
まともに計算しなくても、もとの濃度に対して残した食塩水の割合をかけると早く解決しますよ？というお話でした。もちろんまともに考える姿勢が悪いわけではないです。口ぐせになっちゃってますが算数はポケットの数なんです。ポケットがせまいと広がりにくいですからね。いろいろ知っておくとつながっていくことが多いと思うんですよ。

では今回はこれにておしまいです。食塩水を捨てて同じ量の水を戻す問題に遭遇したら、ぜひこの講座を思い出してくださいね。ではまた次回！