NEWみんなの算数講座75 ついたり消えたり問題

皆さんこんにちは。ニューみん算講座の75回目です。
今回は規則性のジャンルから、電球がついたり消えたりする問題を解説しようと思います。○と×を使って最小公倍数までデータを作るというやり方を覚えておくだけで、枝の問題（カッコ１、カッコ２など）がどんどん解けてしまいますよ。
ではさっそく問題を出してみますね。

最初に書いたように、この手の問題では○と×を使ってデータを準備します。それをしないで計算式だけで解こうとすると、(1)はクリアできると思いますが(2)(3)あたりで必ず苦労します。算数は計算式だけでは役不足！こうした工夫こそが算数のおもしろさなのです。
では僕が作った○×データを見てもらってからまた解説しましょう。

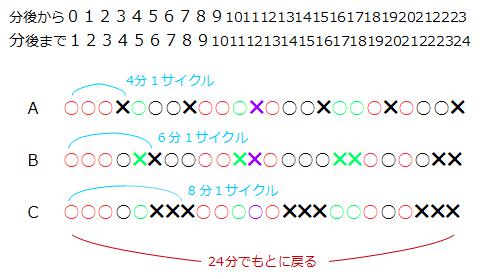
これがデータです。○がついている時間、✖が消えている時間です。
時間の幅がわかるように、単位はつき始める時間（から）とつき終わる時間（まで）を両方書きました。各設問に答えるときは、その状態になった瞬間を答えればよいから、つき始める時間（から）の方で答えます。

僕はこのデータ調査を24分後までで終わりにしました。それはたまたまそうしたわけではなく、きちんと理由があります。

Ａの電球は３分間ついて１分間消えます。その合計の４分間をＡの電球の１サイクル、同じように、Ｂの電球は４分間ついて２分間消えるから合計の６分間を１サイクル、Ｃの電球は５分間ついて３分間消えるから合計の８分間を１サイクルと考えます。
その合計時間４分、６分、８分の最小公倍数は24分だから、３つの電球の状態は、24分後にもとに戻る（スタートの０分後と同じになる）のです。その理由で調査は24分後までで終わりにしました。
このことが(1)の答えになりますね。３つの電球がスタートの次に同時につくのは24分後です。→(1)の答え

(2)
ＡとＣの電球だけがついている状態になるのは、緑色のところです。つき始める時間（から）を読み取ってください。
最初を除いた３回は、４分後、10分後、16分後です。

(3)
Ｃの電球だけがついている状態になるのは、紫色のところです。11分後ですね。データの24分間の中にはこの一回しかありません。しかしそれはデータ調査を24分後までで終えているからです。11分後に24の倍数（24,48,72,…）をたした時刻は11分後と同じ状態です。
次になるのは11分後に24分をたした35分後、その次は11分後に48分をたした59分後です。
解答は11分後、35分後、59分後です。

(4)
すべての電球がついているのは赤のところです。24分間の中に８分間ありますね。
では３時間の中には何分間あるでしょう？
３時間は180分だから、180÷24を計算して、上のデータ図が繰り返される回数を調べます。
180÷24＝７回あまり12分

まず、すべての電球がついている８分間が７回あると考えて
８×７＝56分
さらにあまりの12分間の中に５分間あることがわかります。
※あまりの12分間を調べるときは、図のスタート（０分後）から12分後までを調べます。12分後～13分後にすべての電球がついていますが、12分後までなので、12分後～13分後の１分間は含みません。

56＋５＝61より、求める解答は61分間です。

以上、規則性を見極めて考える電球ついたり消えたり問題でした。理解していただけたでしょうか。
ポイントまとめておきますね。

この問題を通して知ってほしいのは、算数の問題にはいきなり計算を始めてもすぐに行き詰まってしまう問題がある！ということです。(2)や(3)の問題を式を立てて式だけで解決させるのは相当大変だと思います。不可能ではないでしょうがおそらく汗ダクになるでしょうね。算数には長年使われてきたいろいろな工夫があります。NEWみんなの算数講座、すでに75本の講座を書いてきましたが、これからも100本、いやそれ以上を目指して、皆さんに算数の算数らしい考え方をたくさん伝えていきたいと思います。ぜひまた読みにいらしてくださいね。では今回はこれでおしまいにします。お疲れさまでした。