NEWみんなの算数講座107 断頭四角柱

みなさんこんにちは。みんなの算数講座107回目です。

今回は立体図形のジャンルから、断頭四角柱について説明しようと思います。読み方は「ダントウ・シカクチュウ」です。断頭四角柱とは、文字通り、頭を切断された四角柱のことです。
その話に入る前に、ウォーミングアップを１問出しておこうと思います。まずはこの問題から考えてみましょう。

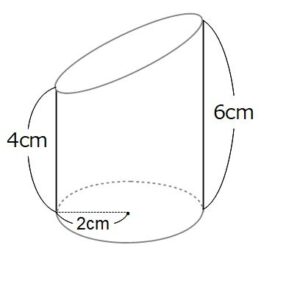
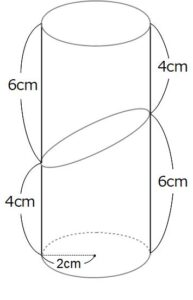これは、パッとひらめいた人も多いと思います。上の断頭円柱と同じものをもう１個持ってきて上に乗せると、高さが10cmの普通の円柱ができます。（上に乗せる合同な立体のことを、少し難しい言葉ですが鏡像といいます。）
円柱の体積は【底面積×高さ】です。半径２cm、高さ10cmの円柱の体積を２で割れば、上の断頭円柱の体積になりますね。
２×２×3.14×10×１/２＝20×3.14＝62.8cm³
これが、上の断頭円柱の体積です。

そして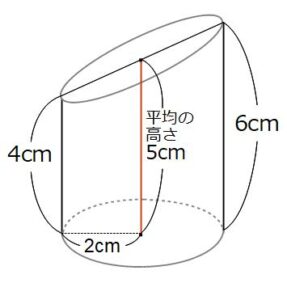このとき、記憶にとどめておいてほしい公式があります。じつはこの断頭円柱の体積は、４cmと６cmの平均の５cmを高さと見ることで計算ができます。この５cmを断頭円柱の平均の高さといいます。
（４＋６）÷２＝５cm…平均の高さ
２×２×3.14×５＝20×3.14＝62.8cm³
断頭円柱の体積＝底面積×平均の高さ

ウォーミングアップ、難しくないですよね？
では続いて今回の本題です。次の問題を見てください。

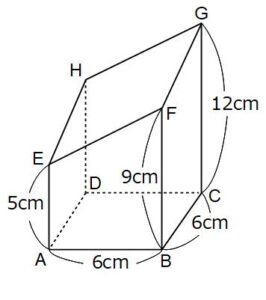
この立体が断頭四角柱です。さきほどの断頭円柱と雰囲気が似てますね。円柱を斜めに切断すると断頭円柱、四角柱を斜めに切断すると断頭四角柱です。
〇〇柱を斜めに切断すると断頭○○柱

(1)
ＨＤの長さは、前面と背面に合同な直角三角形を考えて求めることができます。ＥからＦに至るまでに高さが４cm（９－５）上昇しているから、ＨからＧに至るまでにも、同じように高さが４cm上昇するはずです。
ＨＤの長さは、12－４＝８cmです。
＊切断面の向き合う辺ＥＦとＨＧは平行です。ＨＥとＧＦも同様です。つまり四角形ＥＦＧＨは、２組の向かい合う辺が平行な平行四辺形です。

ここでまたひとつ大事なことがわかります。
断頭四角柱では、向かい合う辺の長さの合計が等しくなります。
ＥＡ＋ＧＣは５＋12＝17cm、ＨＤ＋ＦＢも８＋９＝17cmです。このことを(2)で使います。

(2)
体積は、ウォーミングアップの断頭円柱と同じように、合同な断頭四角柱を上に乗せて考えます。

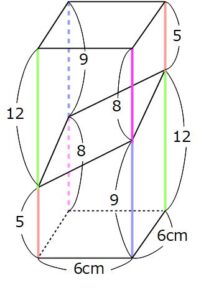
色をつけてみましたが、５cmの上に12cmを乗せ、向かい合う12cmの上に５cmを乗せ、
９cmの上に８cmを乗せ、向かい合う８cmの上に９cmを乗せると、高さが17cmの普通の四角柱（直方体）ができます。
四角柱（直方体）の体積は【底面積×高さ】なので、
６×６×17＝612
これを２で割って、求める断頭四角柱の体積は、
612÷２＝306cm³です。

(3)
さて、いまの体積の求め方を、どうのような公式で残しましょう？
結論としては、断頭円柱と同じように【体積＝底面積×平均の高さ】でよいのですが、
断頭四角柱の平均の高さは、４つの高さ（５cm、９cm、12cm、８cm）の合計を４で割らなくても、断頭四角柱は向かい合う辺の長さの合計が等しくなるので、向かい合う辺の長さの合計（５cmと12cmまたは９cmと８cm）を２で割って求める方が早そうです。

断頭四角柱の体積＝底面積×平均の高さ
＊平均の高さ＝向かい合う辺の長さの合計÷２

もう一度この式で体積を計算すると、
平均の高さ＝（５＋12）÷２＝8.5
断頭四角柱の体積＝６×６×8.5＝306cm³

＊＊＊
以上、断頭円柱と断頭四角柱について解説しました。いかがでしたでしょうか。断頭四角柱は、水を容器に入れて傾けたときの水の形状としてもよく出てきます。
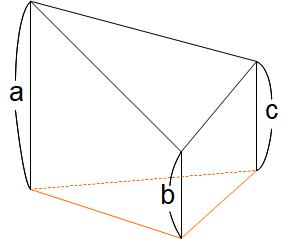
また、今回はくわしく触れませんが、断頭三角柱（右図）という立体もあります。断頭三角柱でも【体積＝底面積×平均の高さ】という公式は使えます。右図の場合、オレンジ色の底面に対して、平均の高さ（ａ＋ｂ＋ｃ）÷３をかければ、体積を求めることができます。ただし、断頭三角柱は、同じものを上に乗せても普通の三角柱はできないから、公式が成り立つ説明は、なかなか大変です。ここでは割愛しますが、機会があればどこかで取り上げたいと思います。

それでは今回の講座はここまでにしたいと思います。次回の講座を楽しみにしていてください。

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
どうぞこちらのフォームからお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら