Newみんなの算数講座10 台形内の平行線(地道と近道)

算数の公式には、絶対覚えなくてはならない算数のルール(約束)と言える必修公式と、覚えていると求める時間が短縮できたりする近道公式があります。
必修公式とは〈長方形の面積=タテ×横〉や〈速さ=距離÷時間〉のように言葉のきまりと言えるものです。きまりを知らなければ算数の舞台には立てませんよね。
一方、近道公式は、知っていると便利だけど、もし知らなくても大ごとにはならない公式です。公式に頼らなくても他の方法でリカバリーできるわけですね。講座4でふれたメネラウスの定理などが近道公式の良い例だと思います。
算数指導者の僕としては、近道公式ばかり教えるのはよくないと思ってます。公式によるショートカットが、算数でもっとも重要な思考の積み重ねを妨害してしまうことがあるのです。たとえてみると、ご当地の高校野球チームが勝ったことを誰かに結果だけ聞くのが近道公式かな。ファンならどういうふうに勝ったのかも気になるでしょう。公式も同じで、いきなり答えが出る式だけ知っていても物足りないだろうし、算数を楽しむことにもあまりならないですね。
しかしその考えをトーンダウンしても教えたくなっちゃう公式はあります。とても美しい公式なのですよ。近道公式もいくつか知っておくのはよいでしょうから、今回は有名な近道公式を一つ紹介しましょう。
では近道公式が使える問題です。
下の図のように、台形ABCDの辺AD、BCに平行な直線EFをひきます。
AD=8cm、BC=20cm、AE:EB=3:2のとき、EFの長さはcmですか?
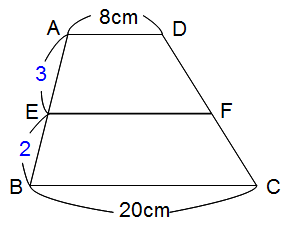
最初は近道公式を使わない地道な解法を説明します。たいていの塾や参考書はこれでしょうね。
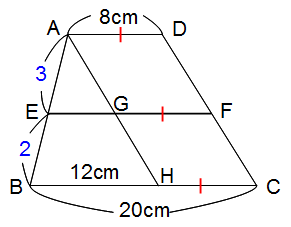
下の図のようにDCに平行な補助線AHを引きます。右側に平行四辺形ができますね。
四角形AHCDは平行四辺形だからGFやHCはADと等しく8cmです。
三角形AEGとABHは相似だから、
EG:BH=AE:AB=3:(3+2)=3:5
BH=20-8=12cmより、EG:12cm=3:5
EG=12cm×3÷5=7.2cm
よって、EF=EG+GF=7.2+8=15.2cm
これが本流のアプローチでした。
メモ
この理解には相似の基本知識が少し必要です。ここでは相似には触れませんから自習をお願いします。
では次に近道公式!今回はこっちが本題でしょうか(^^)/
近道公式
台形内部で上底、下底に平行な線分EFを求める公式は次のようになります。
EF=(X×n+Y×m)÷(m+n)
X、Yは実寸でなくてはいけませんが、m、nは実寸でも比でもどちらでも大丈夫です。
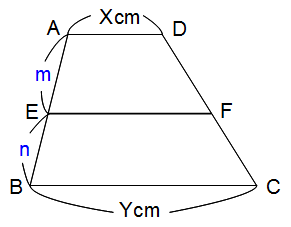
では、さっきの問題でこの公式を使ってみましょう。
(8cm×2+20cm×3)÷(3+2)=76÷5=15.2cm
ね?同じ答えになったでしょう?
上底と下の比をかけ、下底と上の比をかけ、その合計を比の合計でわればおわりです。かけるときにクロスさせる感じが独特だから、一度覚えたらすぐには忘れないでしょうね。
メモ
数学的にはEFの長さをADとBCの長さの加重平均といいます。
台形の近道公式いかがでしたでしょうか?
僕が授業でたまにこうした公式を紹介しますと「こ~ゆ~のもっと教えて~」というリクエストが多いですね。子供でも公式の美しさがわかるのかもしれません。ラクしたいだけかな? まぁ少しなら良いのですが、こうした公式ばかりを教えても、考えない癖がついてしまったりメリットだけではないです。本来公式はその式になる理由も知るべきで、しかし算数では文字式による一般化は容易ではなく、教えたはいいけど理由づけに困るということもあります。
という意味があり、算数では最初に書いた補助線を引く地道な方法がまさるでしょうね。近道公式は、地道な方法が理解できたあとのオマケと思っておくとよさそうです。
では今回はここまでにします。次の講座でまた一緒に算数を楽しみましょう!
みなさんへの宿題
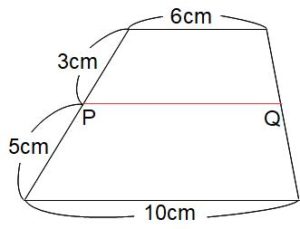
下の図で上底、下底と平行に引いた線分PQの長さは何cmですか。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。