Newみんなの算数講座33 直方体の表面積を小さくする

みなさんこんにちは。この講座もだいぶ回を重ねてきましたが、これからも〈楽しく〉〈親しみやすく〉〈わかりやすく〉をモットーに役に立つ算数を語り続けていきたいと思います。もし気に入ってくれたら、お友だちや知り合いの人にもここを教えてあげてくださいね。よろしくです(^^)/
今回の講座33は立体図形のジャンルです。直方体の体積を固定したままタテ・横・高さを変えていくと表面積がどのように変化するかを調べていきます。同じ体積でも風当たりの強弱はだいぶちがうんですよね。
では問題を出しますね。
1辺の長さが1cmの立方体が24個あります。これらの立方体を積み重ねていろいろな大きさの直方体を作るとき、表面積がもっとも小さくなるのはどのような積み方をした場合でしょうか?タテ・横・高さの3辺の長さで答えてください。
では調査を始めます。立方体を積み重ねて作る直方体のタテ、横、高さの個数を○個、□個、△個とすると、○×□×△=24(個)という式が作れます。
この式は直方体の体積の公式〈タテ×横×高さ〉ですね。ただしこの問題では○、□、△とタテ、横、高さの言葉の対応は重要ではありません。3方向の個数が入れかわっても同じ形の直方体ができるからです。以下、タテ、横、高さという言葉は使わずに解説しますね。
○、□、△は立方体の個数だから整数に限定することができます。大小関係を○→□→△の順に大きくなるとして調べると、○×□×△=24(個)が成り立つのは下の表のA~Fの6パターンがあります。(〇=□のケースもあります)
| 個数○ | 個数□ | 個数△ | |
| A | 1 | 1 | 24 |
| B | 1 | 2 | 12 |
| C | 1 | 3 | 8 |
| D | 1 | 4 | 6 |
| E | 2 | 2 | 6 |
| F | 2 | 3 | 4 |
さて、これら3方向の個数と表面積にどのような関係があるかを計算して調べてみましょう。表面積の計算方法は、次の2つが考えられると思います。
表面積を求める方法①
直方体の表面には〈3種類の長方形が2枚ずつ〉あると考えて計算する。式で書くと
直方体の表面積=(〇×□+□×△+△×〇)×2 ですね。
表面積を求める方法②
全立方体24個の表面にある正方形の枚数(24×6=144枚)から、接着によって隠れる正方形の枚数を引いて計算する。
①が普通で②はちょっとマニアックですかね。この講座ではワケがあって②の方法でも計算しますね。
パターンA
1個×1個×24個の場合です。下の図のように1方向にズラズラ並ぶ棒状の直方体になります。2つの方法で表面積を計算しましょう。
方法①
(1×1+1×24+1×24)×2=98cm2
方法②
23ケ所ある接着部分で2枚ずつの正方形が隠れます。
144-23×2=98cm2
これが最小の表面積ということはなさそうですね。ズラズラと棒状に並べるのはとても風当たりが強く表面積は大きくなります。

パターンBは割愛してパターンCです。
パターンC
1個×3個×8個の場合です。表面積を求めてみますね。
方法①
(1×3+1×8+3×8)×2=70cm2
方法②
タテ方向の接着部分が3×7=21ケ所、横方向の接着部分が2×8=16ケ所。それぞれ2枚ずつの正方形が隠れます。
144-(21+16)×2=144-74=70cm2
パターンAよりは表面積が三割ほど減りましたが、もっと小さくできそうですね。
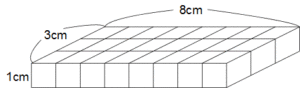
次はパターンEを調べてみましょう。
パターンE
2個×2個×6個の場合です。
表面積 方法①
(2×2+2×6+2×6)×2=56cm2
表面積 方法②
タテ方向の接着部分が2×2×5=20ケ所、横方向の接着部分が2×6=12ケ所、高さ方向の接着部分が2×6=12ケ所。それぞれ2枚ずつの正方形が隠れます。
144-(20+12+12)×2=144-88=56cm2
パターンCよりさらに減り、だいぶ表面積が小さくなってきました。
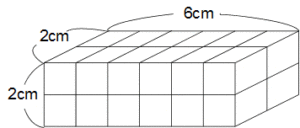
最後にパターンFです。
パターンF
2個×3個×4個の場合です。
表面積 方法①
(2×3+2×4+3×4)×2=52cm2
表面積 方法②
タテ方向の接着部分が2×3×3=18ケ所、横方向の接着部分が3×4=12ケ所、高さ方向の接着部分が2×4×2=16ケ所。それぞれ2枚ずつの正方形が隠れます。
144-(18+12+16)×2=144-92=52cm2
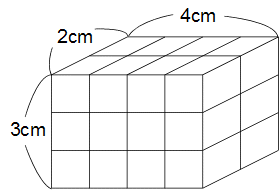
さてみなさんはここまでの調査で、3方向の個数と表面積に何か発見できましたか?
じつは、体積の決まった直方体の表面積を小さくするためには、なるべく立方体に近い形に積み上げればよいのです。その理由は、なるべく立方体に近い形に積み上げた方が立方体どうしの接着部分が多くなるからです。接着部分が増えれば表面積は減りますよね。このことを納得してもらいたい意味があって、表面積の計算で少し面倒な②の方法でも計算しました。
なるべく立方体に近い形とは、言葉を変えるとさきほどの○×□×△=24という式で、○+□+△の和をなるべく小さくするという言い方もできます。下のまとめの表で○+□+△の値を確認してみてください。パターンAの26が最大で、以下徐々に和が小さくなっていき、パターンFの9が最小の和になっています。このとき表面積も一番小さくなるんですね。
次の表は今回の調査結果をまとめたものです。
| 個数〇 | 個数□ | 個数△ | 〇+□+△ | 接着面 の枚数 |
表面積 | |
| A | 1 | 1 | 24 | 26 | 23ケ所 46枚 |
98 |
| B | 1 | 2 | 12 | 15 | 34ケ所 68枚 |
76 |
| C | 1 | 3 | 8 | 12 | 37ケ所 74枚 |
70 |
| D | 1 | 4 | 6 | 11 | 38ケ所 76枚 |
68 |
| E | 2 | 2 | 6 | 10 | 44ケ所 88枚 |
56 |
| F | 2 | 3 | 4 | 9 | 46ケ所 92枚 |
52 |
いかがでしたでしょうか?
同じ体積の直方体で表面積が小さくなるのは〈なるべく立方体に近い形で積み上げたとき〉〈接着部分が多く、内部に隠れる面が多いとき〉〈3辺をたした和が小さくなるとき〉のような言い方ができると思います。なお、接着箇所の数の求め方は、次のような式を用意したので調べてみてください。1ケ所で2枚の正方形が重なるから接着面の枚数は接着箇所のさらに2倍ですね。
接着箇所の数(3辺のひとつから1を引いた積の合計です)
=○×□×(△-1)+○×(□-1)×△+(○-1)×□×△
いやはや今回は長くなりましたね。疲れましたか?僕も書いていて疲れました(笑) では今回はこれでおしまいにしますね。また次の講座でお会いしましょうね!
カーテンコール
お気づきになった人がいるかもしれませんが、もし直方体の各辺の長さが整数でなくてもよいなら、3辺すべての長さが等しくなるとき(つまり立方体になるとき)に表面積は本当の最小になります。その場合の1辺の長さは3回かけて24になる数で24の立方根といいますが、算数ではよほど数値に恵まれない限り立方根を計算することはできません。算数で出題される問題は、この講座のような整数限定なので本当の最小表面積を求めることはありません。参考までに24の立方根は2.8845…らしいです。1辺が3cmを少し下回る立方体のときが表面積は本当の最小なんですね。













