NEWみんなの算数講座97 ベン図で考える倍数の個数

みなさんこんにちは。NEWみんなの算数講座97回目です。あと３講座進むと100講座。記念すべき大台がかなり視界に入ってきました。

今回のテーマは、分数を並べた数列の中で、約分できない既約分数の個数を求めるという問題です。解説の後半では、ベン図を使って倍数や公倍数の個数を計算します。方針が決まればその計算は簡単ですが、問題を見たときは「これって何を計算すればいいの？」と迷う問題だと思います。よく読んで算数らしい考え方をしっかりマスターしてくださいね。では問題を出します。

念のため、既約分数を説明しておきますね。
既約分数とは、分子と分母を同じ整数（１は除く）で割ることができない分数のことです。既約分数の分子と分母は、１以外に公約数を持たない「互いに素」の関係です。
〈例〉
３/５　➡　約分できない（３と５は互いに素）　➡　３/５は既約分数
３/６　➡　約分できる　➡　３/６は既約分数ではない

まさか499個もある分数を１つ１つ調べることはできませんから、何かの法則を見つける必要があります。

求める分数の分母を□、分子を1000－□とします。

(1000－□) / □　←　求める分数

この分数が約分できない既約分数であるためには、
分母の□と分子の(1000－□)が互いに素……☆　であればよいです。

では、□がどのような数のとき、☆が成り立つでしょう？

じつは、□と1000が「互いに素」のとき、☆が成り立つのです。

理由を考えてみましょう。
□と1000に公約数（１以外）があると、その公約数は1000－□の約数にもなっています。つまり、□と1000に公約数があると、□と1000－□にも公約数があることになり、(1000－□) / □ が約分できるから、☆が成り立たなくなります。

説明に文字が入っていると、わかりにくいかもしれませんね。具体的な数で説明すると、650と1000には公約数があります。たとえば50が公約数です。この50は1000と650の差の350の約数にもなっています。650と1000に公約数があると、350/650は約分できる分数になり、☆は成り立ちません。

もう一度まとめます。
(1000－□) / □ が既約分数になるのは、□と1000が「互いに素」のときです。
＊□と1000に１以外の公約数があると　(1000－□) / □　は約分できる分数です。

さて、このことをどう解答につなげるか？もう少しがんばって読んでください。

分母の□は501以上999以下の整数です。この範囲で、□と1000が互いに素になるような□の個数を調べれば、それが問題の解答です。

1000を素因数分解すると、1000＝２×２×２×５×５×５だから、
□が２の倍数か５の倍数のとき、□と1000は互いに素になりません。つまり、□が２の倍数でも５の倍数でもなければ、□と1000は互いに素です。

ここから計算です。
２の倍数でも５の倍数でもない整数の個数を、次のようなベン図を書いて考えてみます。

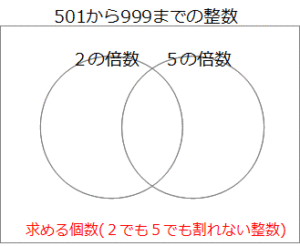
501から999までの整数の個数は、999－501＋１＝499個です。
＊＋１を忘れずに！

２の倍数の個数は　…ベン図の左の輪
999÷２＝499あまり１
500÷２＝250
499－250＝249個
この計算方法についてはあとで書きます。

５の倍数の個数は　…ベン図の右の輪
999÷５＝199あまり４
500÷５＝100
199－100＝99個

２と５の公倍数(＝10の倍数)の個数は　…２つの輪の重なり
999÷10＝99あまり９
500÷10＝50
99－50＝49個

２の倍数、５の倍数の少なくともどちらかに含まれる個数は　…２つの輪の重複を引いた合計
２の倍数の個数と５の倍数の個数をたして、２回数えている２と５の公倍数（ベン図の中央）を引きます。
249＋99－49＝(249－49)＋99＝200＋99＝299個

この個数を全体の個数から引いて、求める個数（501以上999以下の範囲で、２の倍数でも５の倍数でもない整数の個数）は、499－299＝200個　…ベン図の輪の外側
と求めることができます。これが問題の解答です。　

上で何回か使った倍数の個数の求め方。よく使うので整理しておきます。

いかがでしたか？
解説は、上の囲みポイントを説明したかった関係で、分母に注目して501から999の範囲で「２の倍数でも５の倍数でもない整数」を計算しましたが、分子に注目して、１から499の範囲で「２の倍数でも５の倍数でもない整数」を調べても答えは同じになります。範囲が「１から」になるので、こちらの方が簡単ですね。時間がある方は、ぜひ調べてみてください。

では今回はここまでにします。100講座到達も近づいてますので、なるべく早いうちに次回の講座を発表したいと思ってます。それではまた！

カーテンコール
本題には直接関係ないですが、元祖版でこの講座を書いたとき、覆面算を出題していました。今回の改訂でも消さずに残しますね。同じアルファベットに０～９の同じ数字があてはまります。違うアルファベットが同じ数字にはなりません。ぜひ考えてみてください。（解答は次回の講座で）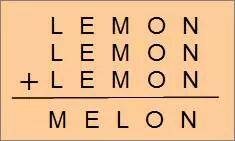

インフォメーションボード

〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。

〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。

〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。

〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら