Newみんなの算数講座11 場合分けのコツをつかもう!

「……となる場合は何通りありますか?」
このようにパターンの数を求める分野を算数では場合の数と呼んでいます。数学では個数の処理という別名もあるようですが、市民権を得ているのは場合の数の方でしょうね。
場合の数の問題を解くとき、次の(A)(B)の区別がポイントになります。
(A)簡単な計算式ですぐに答えが出せる部分
(B)いくつかのケースに場合分けし、それぞれのケースについて調べる作業が必要な部分
(B)のほうが手間も時間もかかるのは言うまでもありません。苦手な人が多いのもテストで差がつくのも(B)でしょうね。しかし(B)こそが場合の数の醍醐味といえるのです。(A)ばかりで終わってしまったらおもしろくないですよね。
では問題を出して解説しますね。最初はカードを並べる問題です。
1、2、3、4と書かれたカードが1枚ずつあります。
これらを並べてできる4けたの整数は全部で何通りありますか?
カード並べの基本問題です。
上位の位から考えると、
千の位→4通り(どのカードを選んでもよい)
百の位→3通り(千の位で使った1枚が減るから)
十の位→2通り(さらに百の位で使った1枚が減るから)
一の位→1通り(さらに十の位で使った1枚が減るから)
よって、4×3×2×1=24通り
一度の計算で答えが出せます。まさに(A)ですね。このかけ算のことを場合の数の積の法則と言いますが、その名前はあまり気にしなくてもよいので、かけ算する感覚を大切にしてください。
0、1、2、3と書かれたカードが1枚ずつあります。
これらを並べてできる4けたの偶数は全部で何通りありますか?
前の問題とは少しアプローチがちがいます。「0が含まれている」ことと「偶数という限定条件がある」からです。このような条件があるときは、一度の計算だけで答えを出すことはできません。(B)の場合分けが必要になります。
偶数だから一の位は0または2です。その2つのパターンに場合分けします。
くわしく 一の位が0のときと2のときではパターン数がちがうのです。そのため、一度の計算でまとめることができません。
〈一の位が0である偶数 □□□0〉
上位の位から考えて、
千の位→3通り(一の位に固定された0を除くから)
百の位→2通り(千の位で使った1枚が減るから)
十の位→1通り(百の位で使った1枚が減るから)
3×2×1=6(通り)←一の位が0の偶数は6通り
〈一の位が2である偶数 □□□2〉
上位の位から考えて、
千の位→2通り(一の位に固定された2と、千の位に使えない0を除くから)
百の位→2通り(千の位で使った1枚が減るが、0が使えるから千の位と同じ2通り)
十の位→1通り(百の位で使った1枚が減るから)
2×2×1=4(通り) ←一の位が2の偶数は4通り
こうして場合分けしたパターン数を合計して、
4けたの偶数は全部で6+4=10通りです。←答え
場合分けをしたときは、それぞれの結果をたして最終的な答えとします。場合の数の和の法則といいますが、この感覚も大切に!
次は色の塗り分け問題です。
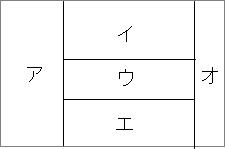
下の図は、先日誕生した新国家サンスーンの国旗ですが、まだア~オに塗る色が決まってません。使える色は赤・青・黄・緑・オレンジの5色ですが、必ずしも5色すべてを使う必要はありません。(すべて使ってもかまいません)
この国旗の色の塗り分け方は全部で何通りありますか?ただしとなり合う区画に同じ色を塗ることはできません。
この問題は、場合分けの感覚を身につけるためにとてもよい問題です。しっかりと読んでいただき、場合分けの感覚を養ってほしいと思います。
問題の条件に「5色すべてを使う必要はない」とあります。つまり、5色すべて使ってもよいし、それ以下の4色や3色で済ませてもいいということです。2色では不可能ですね。
そこで5色使う場合、4色使う場合、3色使う場合に場合分けします。
〈ケース1〉5色で塗り分ける
これはとても簡単です。最初のカード並べの問題と同じように、
アにぬる色 5通り
イにぬる色 4通り(アに塗った1色が減るから)
ウにぬる色 3通り(さらにイに塗った1色が減るから)
エにぬる色 2通り(さらにウに塗った1色が減るから)
オにぬる色 1通り
よって、5色で塗り分ける方法は
5×4×3×2×1=120通りです。
〈ケース2〉4色で塗り分ける
4色の場合はどこかを同じ色にする必要があります。同じ色にするのは
①アとオを同じ色にする
②イとエを同じ色にする
の2通りです。これは区画がとなり合っているから同じ色にできません。
同じ色にするのが①、②のどちらかに決まれば、4色の塗り方が
4×3×2×1=24通りずつあります。
メモ 同じ色になる場所は気にする必要がないでしょうね。
①4色を塗る場所はア、イ、ウ、エ〈オはアと同じだから気にしない〉
②4色を塗る場所はア、イ、ウ、オ〈エはイと同じだから気にしない〉
と考えてください。
そしてもう一点、4色の場合は塗るときに使う色の選び方を考えなくてはなりません。5色から4色を選ぶ方法は5通りです。
くわしく 5色から4色を選ぶことは、使わない1色を選ぶことと同じ。(赤を使わない)(青を使わない)(黄を使わない)(緑を使わない)(オレンジを使わない)の5通り。
以上のことから、4色で塗り分ける方法は、
・4色の塗り方…24通り
・同じ色にする場所を①、②のどちらにするか…2通り
・4色の選び方…5通り
のかけ算となり、24×2×5=240通りです。
〈ケース3〉3色で塗り分ける
3色の場合はアとオ、イとエをどちらも同じ色にするしかありません。3色の場合は同じ色にする場所のパターンは他にありません。3色を塗る場所はア、イ、ウです。(エとオは同じ色にするから気にしないでよいです)
ア、イ、ウに3色を塗る方法は3×2×1=6通りです。
そして塗るときに使う3色の選び方を考えると、5色の中から3色を選ぶ組合せで
5C3=5C2=10通りです。
メモ 異なる□個のなかから△個を選ぶ組合せの計算方法は算数の必須知識です。近々その内容の講座を書く予定です。
3色で塗り分ける方法は、
・3色の塗り方…6通り
・3色の選び方…10通り
のかけ算となり、6×10=60通りです。
以上のことから、サンスーン国の国旗を塗り分ける方法は、
〈ケース1〉 120通り
〈ケース2〉 240通り
〈ケース3〉 60通り
をたし算して420通りとなります。
今回の内容はいかがでしたか?
場合の数には、簡単な計算で寄り切れるとき(A)と、場合分けの作業が必要になるとき(B)があります。おそらくみなさんが気にされるのは、(A)(B)の使い分けだと思いますが、僕からのアドバイスとしては、基本はなるべく(B)の方針で考えるのがよいと思います。そしていろいろ経験していくうちに、この部分は簡単は計算がきくということを感じ取ってほしいですね。
このケースはこう、このケースはこう、このケースはこう、……
そうやって場合分けをして、最後にすべてのパターンを合計する
これが場合の数の問題を解くときの王道です。逆に言うと簡単な計算で済むところがラッキーなんですよね。場合の数はとても奥が深いから、また他の機会にも取り上げてみたいと思います。では次回までごきげんよう!
みなさんへの宿題
下の四国地方の白地図を4色のクレヨンを使って塗り分けたいと思います。4色すべて使っても、3色で済ませてもかまいません。塗り方は全部で何通りありますか?ただし隣り合う県には同じ色を塗れません。
解答したい方はページ下のコメントに書いてください。正解不正解をレスさせていただきます。お名前はニックネームでもかまいません。