NEWみんなの算数講座102 穴をあけると表面積は増える
みなさんこんにちは。NEWみんなの算数講座102回目です。
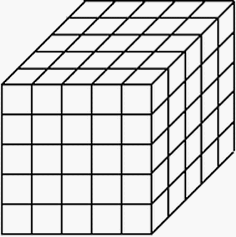今回は立方体に穴をあける問題を解説したいと思います。右の図のように、１辺の長さが１cmの小さな立方体を125個(＝５×５×５)積み重ねた大きな立方体を使って説明します。小さな立方体どうしは接着していて崩れないと考えてください。
では問題を出します。大きな立方体の上面から反対側に貫通するように直方体の穴をあけ、残された立体について体積と表面積を求める問題です。
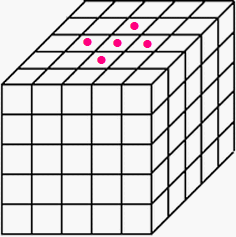右の図のように、１辺の長さが１cmの小さな立方体を125個積み重ねた大きな立方体があります。●印をつけた正方形の面から、反対側の面（底面）まで貫通するように直方体の穴をあけます。穴をあけたあとに残った立体について、
(1)体積は何cm3ですか？
(2)表面積は何cm2ですか？
＊下の図のような底面が十字架（赤十字のマーク）の立体の穴があきます。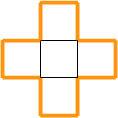
(1)
１方向からのくり抜きだから、体積は簡単です。●印の面１枚につき、上から下まで５個の小立方体がなくなり、●印は５ヶ所だから、全部で５×５＝25個の小立方体がなくなります。
残された立体の体積は125－25＝100cm3です。
(2)
表面積は、体積ほど簡単ではありません。
ところで表面積の意味は大丈夫ですか？
表面積とは「その立体の表面にある面の面積の合計のこと」です。「その立体を水の中に沈めたとき、ぬれる部分の面積の合計」と考えてもよいです。
立体に穴をあけたとき、体積は確実に減りますが、表面積は減るとは限りません。穴のあけ方にもよりますが、表面積は増えることもあります。
立体の穴あけ問題では、表面積は増えることもある！
＊必ず増えるわけではありません。穴をあけることでなくなる面と、新たに生まれる面の大小関係によります。算数の問題では増えるケースがほとんどです。
（最後のカーテンコールもお読みください）
(2)
この問題でも、表面積は穴をあける前より増えることになります。穴をあけることで減る面積と増える面積を比較してみます。
①穴をあけることで減る表面積
穴をあけると、もとの大立方体の上面と底面で表面積が減ります。●印の正方形の面が上面で５面なくなり、底面でも同じように５面なくなるので、合計10面の10cm2が穴をあけたことによって減る面積です。
②穴をあけることで増える表面積
穴をあけることをトンネルを掘るというイメージで考えてください。トンネルを掘ると、トンネルの床、天井、側面の壁に新しく面ができます。この問題は、上面から１方向の穴あけだから、床や天井は現れず、側面の壁だけができます。
穴を上からのぞくと、右の図（再掲）のような形になっています。穴は、この十字架のような形を底面とする高さ５cmの柱体です。
十字架のまわりをオレンジ色で示しましたが、このオレンジ色の部分が上から下までつながるように、長方形の壁面ができます。オレンジ色の壁面を想像してください。その壁面の面積が増える分の表面積です。
オレンジの辺１本に対して、その下に５cm2の長方形（正方形５枚分）の壁面ができ、オレンジの辺は全部で12本あるから、５×12＝60cm2が増える表面積の合計です。
このように穴をあけると、減る表面積（①）と、増える表面積（②）があり、この問題では増える表面積の方が大きいから、その結果、穴をあけたあとの立体の表面積は、もとの大立方体の表面積より増えることになります。
穴をあける前の大立方体の表面積は５×５×６＝150cm2だから、ここから①を引いて②を加え、穴をあけたあとの立体の表面積は、150－10＋60＝200cm2です。
＊＊＊
以上、立方体の穴あけ問題を解説しました。今回は１方向からのシンプルな穴あけなので、それほど難しくなかったと思います。穴あけ問題には、あける穴が１方向からだけではなく、「上から」「前から」「横から」のように３方向から穴をあける問題もあります。その場合は、大立方体の内部で穴と穴が衝突し、体積ではその分のダブりを引かなくてはなりませんし、表面積では壁以外に天井や床も現れ、ふきぬけになっている部分では、面が消えてしまうこともあります。そうなるとけっこうややこしい問題です。近いうちにそんな問題も解説できればと思います。
では今回の講座はここまでにします。次回の講座で、またいっしょに算数を楽しく勉強しましょう。次回は推理の問題を予定しています。
カーテンコール
全体の形が立方体のとき、穴あけによって「増える面積」は「減る面積」より必ず大きくなります。つまり、全体の形が立方体の穴あけでは、表面積は必ず増えます。もし表面積が減るとしたら、全体の形が背の低い直方体の場合でしょう。それなら「増える面積」を「減る面積」より小さくすることもできますね。しかし、表面積が減る穴あけ問題を僕は一度も見たことがありません。穴あけ問題では表面積は増えると思っていて大丈夫でしょう。
インフォメーションボード
〈算数の家庭教師のご相談・ご依頼・体験授業〉
こちらの説明ページをお読みいただき、ページ内のフォームからご連絡をお願いします。
〈お仕事関係のご連絡〉
こちらの連絡用フォームからお願いします。
〈算数講座へのご意見や質問／ウタマル先生へのお便り〉
こちらのフォームからどうぞお寄せください。
〈全講座カラー印刷ファイル〉
おかげさまでとてもよく売れています。どうもありがとうございます。印刷屋さんの協力で、５講座ずつを１冊子にまとめ、「なかとじ印刷」した片側Ａ５サイズ（開くとＡ４）のコンパクト版です。内容やご注文方法は、ご案内ページをご覧ください。
ご案内ページこちら
