NEWみんなの算数講座76 死も苦しみもない世界

皆さんこんにちは。ニューみん算講座76回目です。

今回の講座では、Ｎ進法を使ったとても面白い問題を紹介します。Ｎ進法の基礎については第50～51講座に書きましたから、N進法の基礎に自信がない人は、先にそちらからお読みください。N進法の基礎がわかってないと、今回ついてくるのは大変だと思います。

では話を始めます。

人間に生まれた以上、死や苦しみはつきものです。アウストラロピテクスの時代から現在に至るまで何百万年、死をまぬがれ、永遠の命を授かった人間はひとりとしていません。残念ながら人間には寿命というものがありますからね。
＊アウストラロピテクス…アフリカで生まれた初期の人類。200-400万年前。くわしくはこちらからどうぞ！

いきなりこんな話をしたら「あれ？今回は算数の講座じゃないの？」
と思われてしまいそうですが、ご心配なく！ちゃんと算数なんです。算数の世界には死も苦しみもない世界があるんですよ。ホントかって？　はいホントです。
では死も苦しみもない世界を下に書いてみますよ？

１、２、３、５、６、７、８、10、11、12、13、15、16、17、18、20、
21、22、23、25、26、……、37、38、50、51、52、53、55、56、……、
87、88、100、101、102、103、105、106、107、108、
110、111、112、113、115、116、……

はい、これが死も苦しみもない世界です。
わかりますか？
数を１から順に並べましたが、死（４）と苦（９）を用いる数がすべて抜いてあります。僕は別にふざけてませんからね。これ、大まじめな算数の題材なんです。

ではこれから死も苦しみもない問題を出しますが、今書いたような数の並べ方を病院方式と呼ぶことにしましょう。病院は縁起上の配慮から、一の位が４や９の部屋、104号室や209号室を作りませんからね。
(注)ここでの病院方式は、すべての位に４と９を使いません。 つまり４と９は数字として存在しないのです。病院では「一の位」に４と９を使わないだけだから、病院の部屋番号とここでの病院方式は同じではありませんが、イメージとして病院方式と呼ぶことにします。

では問題いきます。

変更前の料金が15000円より安いことはわかりますね？
なぜなら、変更後の病院方式は４と９という数字を使わないから、そのぶん数の進み方がはやくなり、15000という数は変更する前よりはやく現れるはずだからです。

この問題、じつは８進法の問題なんです。８進法は８個の数字で数を表していく方法のことです。

そしてここが少しややこしいのですが、ふつう８進法では０～７の８個の数字を使います。しかし病院方式の８進法は４と９を除いた〈０１２３５６７８〉という８個の数字を使うのです。普通の８進法と病院方式の８進法で使う数字を対応させると次のようになります。

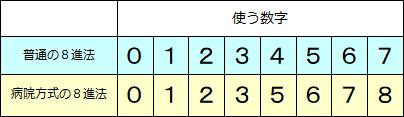
９がないことはどちらも同じですが、病院方式の８進法には４がないから、上のように普通の８進法の４～７が、病院方式の８進法では５～８となり、１つずつズレが生じています。

それでは解答を求めましょうか。
病院方式の８進法で表された15000は、いま説明した使う数字の違いから、普通の８進法なら14000です。
＊病院方式の８進法の５は、普通の８進法の４（上表参照）

したがって、８進法の14000を10進法に直せば解答が求められます。国会での変更前は僕たちがいつも使っている10進法ですからね。

８⁴×１＋８³×４＝4096×１＋512×４＝4096＋2048＝6144より、
病院方式（国会での変更後）で日本人が払ったタクシー代の15000円は、変更前の僕たちがいつも使っている10進法では6144円だったことがわかります。
＊８⁴は８×８×８×８の意味です。（第50～51講座参照）

死も苦しみもない算数の世界、いかがでしたでしょうか？
たった数字が２個減っただけで、6000円ちょっとが15000円になるなんて、なんか意外な感じがしますね。僕も問題を考えたとき、もう少し15000円に近い答えかと予想しました。でもしっかり計算しましたよ。6144円で合っています。

簡単？　そう思った人はＮ進法がよくわかっているから安心して大丈夫ですよ。
難しい？　もう一度Ｎ進法の基礎をよく振り返ってみてくださいね。

それでは今回の講座はこれで終わりにしようと思います。次の講座、なるべく早く発表できるようにしますね。ではではまた。